5. Lists

5.1. List Operations

Yay! Finally, we get to talk about lists. Lists are very useful and powerful structures in Python, and their use is critical when we start working with real-world data. So, let’s get cracking!

Let’s motivate the need for lists. Suppose I wanted to write software that keeps track of students’ names and test scores. Let’s store their names first. Given what we know so far, we would need a separate variable for each student name.

student1 = "John Smith"
student2 = "Judy Adams"
student3 = "Frank Johnson"

If we had another student enroll in the class, we’d need to add another variable.

student1 = "John Smith"
student2 = "Judy Adams"
student3 = "Frank Johnson"
student4 = "Paige McConnell"

How many variables do we need? Well, I guess we’d need as many as we think we might possibly need. If we were using this software at a large public university, we might have 500 students in a Computer Science 1 class, so our code might look like this:

student1 = "John Smith"
student2 = "Judy Adams"
student3 = "Frank Johnson"
# ...
# ...
# ... definitions for student4 through student498 omitted ...
# ...
# ...
student499 = "Sally Schmidt"
student500 = "Maxwell Masterson"

That’s a lot of variables, and this is getting ridiculous.

What if instead of a whole bunch of variables to store all of our students, we could have just one variable to store all of the students. We can! Contrast the code we’ve presented so far with the code in Listing 5.1.

Listing 5.1 First list example

students = ["John Smith", "Judy Adams", "Frank Johnson", "Paige McConnell"]

The students variable holds a list of values. In this case, each value is a single string value, and there are four strings stored in this list. We use the square bracket symbols [ and ] when we want to create a list.

In Listing 5.1, whenever we want to store more students, we don’t need to create more variables. We can just dump their names into this students variable. Cool, huh? Actually, we haven’t even scratched the surface of how useful this is going to be.

So, what can we do with a list once we’ve made one? Table 5.1 shows several handy list expressions and list functions. To make sense of the table, suppose we have the following variables.

Let...
   L be a list,
   L1 be a sub-list of L,
   v be a value we wish to store in a list,
   i be an index integer,
   j be another index integer,
   s be a string, and
   p be a string

You’ll notice in Table 5.1 that some of the same operations that can be performed on strings can also be performed on lists.

Table 5.1 Expression/value/type

Expression	Explanation
v = L[i]	The indexing operator: gets the ith item from L and places it in the variable v.
L1 = L[i:j]	The slicing operator: makes a new list L1, which is a sub-list of L consisting of L’s items from index i up to–but not including–index j. Both i and j may be omitted. If i is omitted, the beginning of the list is assumed. If j is omitted, the end of the list is assumed.
L.append(v)	Adds the value v to the end of the list L.
L.insert(i, v)	Inserts the value v into the list L at position i.
L.remove(v)	Removes the first instance of the value v in the list L. If there are more instances of v in L, they will be ignored. If v does not exist in L, the program will trigger a ValueError.
v = L.pop(i)	Removes the value in L at index i and places it in the variable v. i may be omitted, in which case the last item in the list is removed.
L = s.split()	Uses the parts of a string to make a list. Does so by splitting a string up into pieces separated by whitespace and placing the resulting items into the list L. It does not modify the original string s.
L = s.split(p)	Uses the parts of a string to make a list. Does so by splitting a string up into pieces separated by the string pattern p and placing the resulting items into the list L. It does not modify the original string s.
s = p.join(L)	Joins the items in the list L to form a new string (stored in s) by joining the items together with the string p.

The more you program, the easier it will become to read tables like Table 5.1. For most beginning programmers, however, it is easier to learn by looking at examples. Listing 5.2 demonstrates a few “toy” examples of how to use these list operations. The result of most of the operations is printed, and the effect of each statement is shown in a comment to the right of the statement.

Listing 5.2 List operations example

cheeses = ["cheddar", "swiss", "feta", "gouda", "parmesan"]
line = "red,green,blue,teal,cyan"

print(cheeses[1])           # prints swiss
print(cheeses[0:2])         # prints ["cheddar", "swiss"]
print(cheeses[-1])          # prints parmesan
print(cheeses[3:])          # prints ["gouda", "parmesan"]
print(cheeses[:2])          # prints ["cheddar", "swiss"]

cheeses.remove("parmesan")  # cheeses is now ["cheddar", "swiss", "feta", "gouda"]
cheeses.pop(-1)             # cheeses is now ["cheddar", "swiss", "feta"]
cheeses.pop()               # cheeses is now ["cheddar", "swiss"]
cheeses.append("jack")      # cheeses is now ["cheddar", "swiss", "jack"]
cheeses.insert(0, "brie")   # cheeses is now ["brie", "cheddar", "swiss", "jack"]

colors = line.split(",")    # colors is now ["red","green","blue","teal","cyan"]
print(len(colors))          # prints 5
print(", ".join(colors))    # prints red, green, blue, teal, cyan
print(" -> ".join(colors))  # prints red -> green -> blue -> teal -> cyan

Okay, let’s test our understanding by trying to apply what we’ve learned. Suppose we have a list named lst defined as:

lst = ["Maria", "Sheryl", "Barbara", "Shafi"]

Can we write code to modify lst so that the first item is moved to the end of the list? In other words, the end result should look like this:

lst = ["Sheryl", "Barbara", "Shafi", "Maria"]

We can use any number of statements that we want. Try it. Try mocking up a solution using comments first, and then write your code beneath each of the comments.

Here’s one approach. First, let’s start with comments.

# Remove the first item and store it.

# Put the stored item on the end of the list.

Now, let’s fill in the details of how we accomplish these steps.

# Remove the first item and store it.
value = lst.pop(0)

# Put the stored item on the end of the list.
lst.append(value)

Good! This is a suitable way to accomplish this task, and more importantly, it is easy to read what the code does even if there are no comments to explain the statements. To see what I mean, let’s strip away the comments.

value = lst.pop(0)
lst.append(value)

We can clearly see that the first statement extracts the first item, and the second statement puts it back on the end of the list. We should always try to write our code in such a way that it is easily read and understood. This was best articulated in the preface of the book Structure and Interpretation of Computer Programs (a.k.a. “SICP”) by Harold Abelson and Gerald Sussman:

"Programs must be written for people to read, and only incidentally for machines to execute."

We could have also written this code as a one-liner, like this:

lst.append(lst.pop(0))

One could argue this is harder to read, at least initially.

Let’s try another example. What if we wanted to “swap” the locations of the first and second items in the list, regardless of what the values in those locations happen to be? Consider the following definition of lst.

lst = ["Maria", "Sheryl", "Barbara", "Shafi"]

Can we write code that makes lst look like this?

lst = ["Sheryl", "Maria", "Barbara", "Shafi"]

Try to write code that does this. Make a good, honest attempt before reading ahead.

We know that we want the value of the expression lst[0] to be changed to the value of the expression lst[1] and vice versa. So, our first attempt might be Listing 5.3.

Listing 5.3 First attempt at swapping value in a list

lst[0] = lst[1]
lst[1] = lst[0]

Consider the effect of the first statement lst[0] = lst[1], which is shown in Figure 5.1.

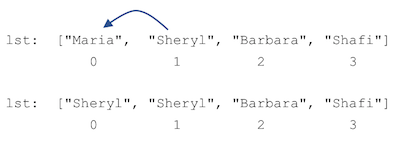
Fig. 5.1 Incorrect attempt at swapping values in a list

Uh oh! Our first statement overwrites “Maria” and she disappears forever! That is not good at all.

What we need to do is save “Maria” somewhere first so she doesn’t get obliterated. So let’s create a temporary variable – a one-use variable that will help us accomplish a task, and then we’ll likely never use it again. Think of a temporary variable (or just “temp variable” for short) like a Post-It note. We may write something on a Post-It note to remind ourselves of something for a brief period of time. Consider our next attempt in Listing 5.4.

Listing 5.4 Correctly swapping values in a list

temp = lst[0]
lst[0] = lst[1]
lst[1] = temp

Let’s visualize how this works (see Figure 5.2).

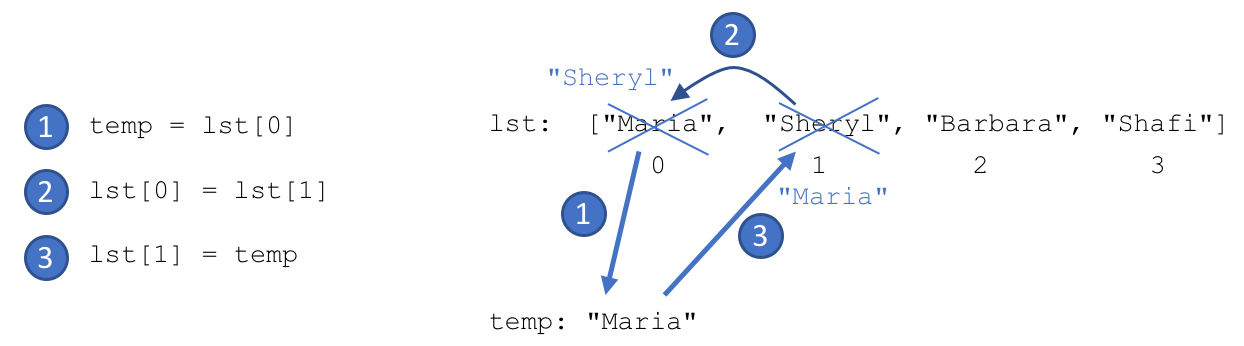
Fig. 5.2 Swapping values in a list

The statement labeled number 1 copies the value at index 0 (in this case, "Maria") into the temp variable for safe keeping. Then, statement number 2 writes the value at index 1 over the top of the value at index 0. At this point (after executing statement number 2), there are two “Sheryl” strings in the list, but that’s okay because we have saved "Maria" in our temp variable. Finally, in statement number 3, we take the value saved in temp and we overwrite the value in index 1 with temp’s value. The list contents are now correctly ["Sheryl", "Maria", "Barbara", "Shafi"].

Index 0 and index 1 are hardcoded in Listing 5.4. If we wanted, we could invent two variables i and j to hold the indices whose values we wish to swap (see Listing 5.5).

Listing 5.5 Swapping values in a list, no hard-coded indices

i = 0  # or, whatever index we wish
j = 1  # or, whatever other index we wish
temp = lst[i]
lst[i] = lst[j]
lst[j] = temp

5.2. Assignment Statements Revisited: Multiple Assignment

Since this book is purely an introduction to programming more so than a definitive guide to the nuances of Python, we could stop our discussion right here. This same programming technique will work with most other programming language as you encounter them (e.g., C++, Java, etc.). However, Python has a really cool way of performing swaps called multiple assignment that your author (that’s me!) simply can’t help himself from showing you! We can replace the code in Listing 5.5 with Listing 5.6.

Listing 5.6 Swapping values in a list using multiple assignment

i = 0  # or, whatever index we wish
j = 1  # or, whatever other index we wish
lst[i], lst[j] = lst[j], lst[i]

Wizardry!

How does this work? Let’s approach it visually as in Figure 5.3.

Fig. 5.3 Multiple assignment

Multiple assignment is a Python feature known in the computer science community as syntactic sugar. Syntax is how you arrange a statement so that it can be understood. In the English language, sentences have a syntax consisting of a noun phrase followed by a verb phrase followed by terminating punctuation (like a period or exclamation point). That’s how we start parsing (or “breaking apart and making sense of”) a sentence. “Sugar” in this case means non-essential. So, syntactic sugar refers to language features that make something easier or more expressive but are non-essential. Usually, syntactic sugar is converted by the compiler behind the scenes to another form through a process called desugaring. If you continue on in studying computer science, this won’t be the last time you hear about desugaring, hopefully.

Desugaring in this case first evaluates the expressions on the RHS, and then converts this

lst[i], lst[j] = "Sheryl", "Maria"

behind the scenes into this

lst[i] = "Sheryl"
lst[j] = "Maria"

5.3. List Variables: References Versus Values

Here is some fairly simple code that creates variables, changes one of them, and then prints their values.

Listing 5.7 Simple assignment statements

x = 3
y = x
x = x + 1
print(x)   # prints 4
print(y)   # prints 3

Let’s do something similar, only this time we’ll use lists of numbers.

Listing 5.8 Assignment with list variables

xlist = [2, 4, 6]
ylist = xlist
xlist.append(8)
print(xlist)
print(ylist)

You may have expected the first print statement to yield [2, 4, 6, 8] and the second one to yield [2, 4, 6], but that isn’t what happens at all! Instead, the output is:

[2, 4, 6, 8]
[2, 4, 6, 8]

How is it that changing xlist has the side-effect of changing ylist? What is this sorcery?!

The good news is that the reason is really fairly simple, especially when we explain it with pictures. Consider the first example in Listing 5.7 where we had integer variables x and y (see picture in Figure 5.4).

Fig. 5.4 Visualizing Listing 5.7

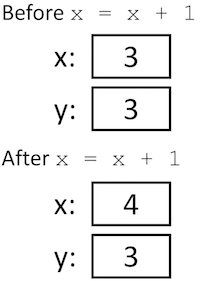
No surprises there. Now, let’s see what happens in the example with xlist and ylist. It turns out that list variables don’t actually contain lists themselves. Instead, they contain something called a reference to a list. The list is actually stored somewhere else. Think of a reference as being like a “pointer” or an arrow to somewhere else in the computer’s memory. With this in mind, we can represent the code in Listing 5.8 visually in Figure 5.5.

Fig. 5.5 Visualizing Listing 5.8

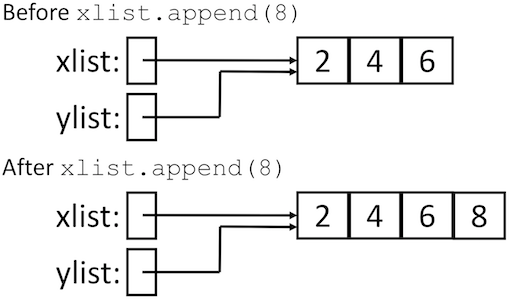
If we attempt to modify xlist or ylist, either will affect the same list. You might ask why this happens in Python, and there is a perfectly good reason that we will explore in Section 5.4. For now, recognize that we want to know how to make ylist be a copy of xlist. We could do the following.

ylist = xlist[:]    # the right way to make a copy of a list

This code assigns a slice of xlist to the new variable ylist. Why no integers before or after the colon (:)? Recall that the integers around the colon are optional. If no integers are given, it selects the entire list. The end result is shown in Figure 5.6.

Fig. 5.6 Copying a list using the slicing ([:]) operator

Now if we perform xlist.append(8) this time, we end up with the result in Figure 5.7.

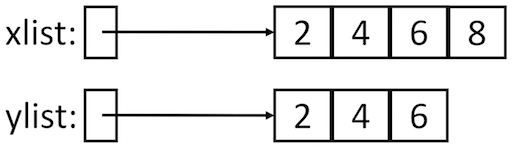
Fig. 5.7 Appending an item after copying the list

5.4. Functions with Lists

In the previous section, we learned that list variables do not contain the lists themselves. Rather, they contain a reference to a list. There are a number of perfectly good reasons for this, the first of which has to do with how functions interact with lists.

Let’s consider an example. Suppose we have a list of strings that happen to be integers, like ["1", "2", "3", "4"]. We wish to change the list so that the values are actually integers rather than strings, that is, [1, 2, 3, 4]. We would need to pass the list to the function as an argument.

def make_int_list(lst):
    # function body goes here


# main section of code
numbers = [ """Somehow we get a bunch of strings here.""" ]
make_int_list(numbers)
# Now 'numbers' has been changed from a list of strings
# to a list of integers.

We have named the parameter lst, but you can name it whatever seems appropriate. We named it lst rather than list since the word list is already used in Python as the name of a type.

As we learned in Section 4.2, Python passes arguments to function parameters by value. That is, a copy of the value in the main program is sent to the function. Imagine if list variables contained the lists themselves rather than “references” to the list. Let’s examine the fall out if that were the case. In the above example, a copy of the numbers list would be sent to make_int_list, so lst would be a complete copy of numbers (see Figure 5.8).

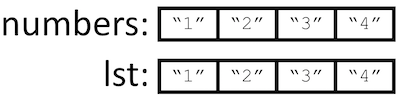
Fig. 5.8 Variable lst if list variables contained the list itself (rather than a reference)

If we program properly, make_int_list would convert all the strings in the list to integers so the end result would be as shown in Figure 5.9.

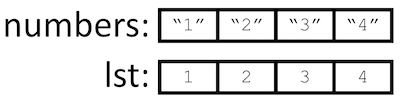
Fig. 5.9 Desired result of make_int_list

But, the original list that we wanted to change, namely numbers, hasn’t changed as we would like!

Now, consider what happens since list variables contain references to lists instead of the actual lists themselves. The reference is passed by value, so lst now “points” at the same list as numbers (see Figure 5.10).

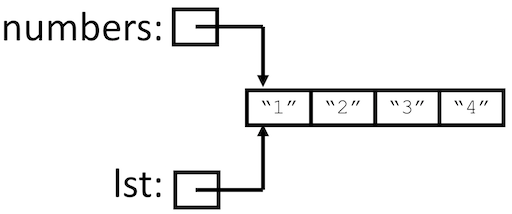
Fig. 5.10 List reference passed to make_int_list

Now when make_int_list has returned, all changes made to lst are also made to numbers because both lst and numbers refer to the same list (see Figure 5.11)!

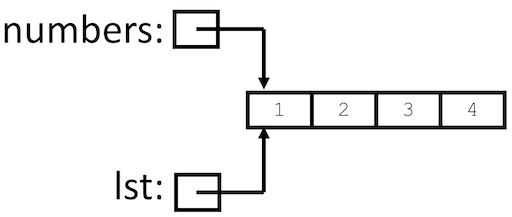
Fig. 5.11 make_int_list makes changes to the list

We should probably go ahead and write the function’s body. We use a loop to walk through each index. At each index, we can convert the string to an int.

def make_int_list(lst):
    for i in range(0, len(lst)):
        lst[i] = int(lst[i])

That’s it!

There is another advantage to passing a list to a function given that lists are stored by reference rather than by value. Suppose we had a very large list of information (say, 500 million strings). If the entire list was passed to the function rather than just a reference to the list, Python would have to make a copy of the entire list, all 500 million items. That takes precious time, and even though computers are fast, there are limits even to what computers can do (more on this in a later chapter). It also uses an unnecessary amount of memory, because now instead of having one list containing 500 million strings, we now have two lists containing a cumulative total of 1 billion strings. There are some computer languages that let you pick whether you pass arguments to functions by value or by reference no matter what the type of the variable is. It is common practice in those languages to pass large lists by reference for that reason alone.

Let’s look at another way we might use functions on lists. We won’t always define functions that modify lists directly. Sometimes, we will pass a list to a function, and then the function will return a value or an entirely new list based on the original list. For example, there is a function named sum that takes a list of numbers and returns the sum of all the numbers in the list. We could use it like this.

money = [30.50, 72.25, 10.00]
grand_total = sum(money)
print("You have $%.2f." % grand_total)

sum takes a list as a parameter and returns a float. It does not modify the list in any way. How did the person who wrote the sum function do it? Let’s find out by writing our own, only we need to give ours a different name. Let’s call it total. Once we define our function named total, we will be able to do this.

money = [30.50, 72.25, 10.00]
grand_total = total(money)
print("You have $%.2f." % grand_total)

Let’s begin. We know that we need the name of the function to be total, and it needs to accept a single list parameter, so we can write:

def total(numbers):
    # function body goes here

Now, the function body will need to loop through the list of numbers and add each of them to a variable. The variable will keep track of the running total. So, let’s create the variable (we’ll call it running_total) and then write the loop.

Listing 5.9 Function definition for total

def total(numbers):
    running_total = 0.0
    for i in range(0, len(numbers)):
        running_total += numbers[i]
    return running_total

This should work. Go ahead and test it out. The key ideas here are:

1. We’re passing a list to a function.

2. We’re using a loop to walk through the list’s items.

3. We’re creating a variable that we will update in each iteration of the loop.

These key ideas will show up a lot when we write functions that operate on lists.

Let’s try out a different example, and let’s see if we can apply some of the same ideas mentioned in the prior paragraph. Suppose we have a list of numbers. We want to know the smallest value in that list of numbers. Let’s write function that determines this for us.

First, let’s pick a name for our function: smallest.

Next, let’s write the function signature.

def smallest(numbers):
    # FIXME

Notice how I have a comment with the all-caps word FIXME in place of the function’s body? This is a common idiom that programmers use to remind them that they need to add code to a particular part of a file. I suppose it’s silly to do this since we’re going to replace the function body very shortly, but it’s worth bringing up since 1.) many programmers do this, and 2.) many programs for editing code will keep track of your FIXME’s and then help you find them before you test out your code.

Okay, now let’s use a loop to walk through the list’s items as we described above. We’ll use a variable to keep track of the smallest value we’ve seen so far with each step of the loop.

Listing 5.10 Function definition for smallest, first attempt

def smallest(numbers):
    small = 0.0
    for i in range(0, len(numbers)):
        if numbers[i] < small:
            small = numbers[i]
    return small

It’s kind of crazy how similar smallest is to total, isn’t it? In computer science, we take a whole bunch of problems (many of them very complicated) and rearrange them so we can apply simple solutions to them. That’s one of the cool things about computer science; it teaches us to define and organize our problems so that we can manage the complexity of the problem. Yay computer science!

Okay, let’s not pat ourselves on the back too much here. We haven’t tested this code yet. Let’s try it out.

print(smallest([5, -5, 2, 3]))
print(smallest([10, 30, 20]))

The output of these tests is:

-5
0.0

The first line is correct. The second line is BOGUS! What went wrong? Can you figure it out on your own? (Sure you can. Take a deep breath and debug it.)

The problem is on line 2 of Listing 5.10. We needed to give the variable small a good first value, but we weren’t sure what a good first value was at the time. We picked 0.0. Unfortunately, nothing in numbers is going to be smaller than 0.0 when all the numbers are greater than zero, so smallest returns 0.0 even though there is no zero in numbers.

So, what would be a better starting choice for small than zero? Some students might say, “How about a really big number!” That’s not a bad idea. We could do something like Listing 5.11.

Listing 5.11 Function definition for smallest, second attempt

def smallest(numbers):
    small = 1000000000.0
    for i in range(0, len(numbers)):
        if numbers[i] < small:
            small = numbers[i]
    return small

This will work really well… until we have all numbers that are bigger than 1 billion.

Let’s try one more strategy. Let’s let the first smallest number be the first number in the list. Suppose numbers[0] is 10.0. Then, the first value of small can just be 10.0. This should work nicely. If the first number in the list is the smallest, small will stay set to that number. If there is a smaller number down the line in the list, eventually it will get changed. This should work, and our final function definition for smallest is shown in Listing 5.12. Naturally, we’ll want to test it, however.

Listing 5.12 Function definition for smallest, corrected

def smallest(numbers):
    small = numbers[0]
    for i in range(0, len(numbers)):
        if numbers[i] < small:
            small = numbers[i]
    return small

This final code works… as long as there is at least one item in the list. If the list is empty, then calling smallest doesn’t make much sense in the first place. After all, a list with no items does not have a smallest item, per se.

Are these examples starting to help? How about if we do a few more examples?

Here’s a different one. Suppose we have a list of student exam percentages. Such a list might look like this (we’ll call it scores):

scores = [82.5, 77.0, 95.0, 56.0, 74.5, 46.0, 97.5]

In this example, there are seven student scores. We could think of other examples where there could be far more scores. Suppose we’re interested in the number of students who passed the exam, i.e., the number whose score is 60 or above. Let us define a function named number_passed that returns the number of passing students.

First, write the function signature (Listing 5.13).

Listing 5.13 Function signature for number_passed

def number_passed(scores):
    # FIXME
    pass

I’ve written pass for the body of the function. We’ll delete it very shortly, but I thought now would be a good time to introduce pass. What does pass do exactly? Python expects there to be an indented block of statements after a function signature. If there is no indented statement or block of statements, our code will crash. Comments don’t count, so naturally FIXME comments don’t count either. This way I can still run any other code in my file even if I haven’t finished the definition of number_passed.

Okay, let’s delete the pass statement and the FIXME comment and replace them with an actual function body. What are we trying to accomplish again? We want to scan the list and keep track of how many students passed. Any time we need to scan a list, we should immediately think of using a loop. We’ve used for loops mostly, but we can use while loops just as easily. It’s up to you as the programmer to express your code however you want. Let’s write some code that scans through the list. Listing 5.14 shows a loop with a lot of pseudocode surrounding it.

Listing 5.14 Partial function definition for number_passed, attempt 1

def number_passed(scores):
    # Probably use a variable to keep track of something.
    for i in range(0, len(scores)):
        # Do something with scores[i]
    # Return a thing.

This function definition follows the same pattern as total and smallest. Since we wish to keep track of the number of students who’ve passed, we’ll use a variable and that variable’s value will be what this function returns. Let’s update those lines (Listing 5.15).

Listing 5.15 Partial function definition for number_passed, attempt 2

def number_passed(scores):
    passed = 0
    for i in range(0, len(scores)):
        # Do something with scores[i]
    return passed

Notice how we’re writing the code non-linearly. Often, it’s best to write what you can at the time, use comments when you’re not ready to fill in the details, and then go back later and fill in the details. Otherwise, it’s easy to get lost in the details.

Lastly, we need to increment passed whenever we encounter a passing score, i.e., scores[i]. Checking scores[i] involves an if statement (Listingref{code:number_passed_final}).

Listing 5.16 Function definition for number_passed

def number_passed(scores):
    passed = 0
    for i in range(0, len(scores)):
        if scores[i] >= 60.0:
            passed += 1
    return passed

This looks simply grand! Now, you test it!

Write some test cases. Use the examples of test code that we’re written in previous examples. Go ahead. I’ll wait. I could use a break from writing this book. Writing a book is hard work, you know.

Okay, I’m back. Did you come up with something like this?

print(number_passed([5, 100, 2, 70]))    # should print 2
print(number_passed([90, 80, 70, 60]))   # should print 4
print(number_passed([1, 2, 3]))          # should print 0
print(number_passed([]))                 # should print 0

5.5. Using Several Lists to Store Related Data

We’ve been using lists thus far to store groups of related information. In Section 5.4, for example, we kept a series of exam scores in a list variable we named scores. We might store a series of names in a list called names.

But, what if we want to keep track of both names and scores. That is, we want to associate students’ names with their scores. In this way, we can know that Michelle got a 90% while Susan got a 76%. There are a number of ways to accomplish this, and in fact we will explore some rather slick ways to do this in Chapters 7 and 9 respectively. However, there is a very good way to do this by simply using more than one list. Observe Listing 5.17.

Listing 5.17 Using several lists to store related data

names = ["Aubrey Bell", "Adam Jamison", "Susan Stratford", "Michelle Wang"]
scores = [82.5, 87.0, 76.0, 90.0]

Notice that names and scores contain the same number of items. Let us assume that the positions of each name matches the position of the score in each list. For example, "Aubrey Bell" got an 82.5 since both values exist at index 0 in both lists. Likewise, Susan Stratford got a 76.0 because they are both at index 2 in both lists.

In the example found in Listing 5.17, we are using different lists to store different attributes of people. Each list has the same number of items. One attribute is the person’s name, which is stored in its own list. Another attribute is a person’s score, which is stored in its own list as well. Each person is uniquely identified by an index. Figure 5.12 shows this relationship appears visually, using indices to associate names and scores. (Note: not all items and indices are shown in the figure to keep the image smaller).

Fig. 5.12 The relationship between values in two lists

The definitions in Listing 5.17 allows us to write code like the following (see Listing 5.18).

Listing 5.18 Iterating through related lists

for index in range(0, len(names)):
    print("The score for %s is %.2f%%." % (names[index], scores[index]))

The output of the example code in Listing 5.18 is:

The score for Aubrey Bell is 82.50%.
The score for Adam Jamison is 87.00%.
The score for Susan Stratford is 76.00%.
The score for Michelle Wang is 90.00%.

5.6. Coding Conventions for Lists Spanning Multiple Lines

Sometimes the lists we define will have a whole lot of items, and it will be cumbersome to manage their contents on a single line. We can “spread out” the definition of such a list using the convention shown in Listing 5.19.

Listing 5.19 List definition spanning multiple lines

cheeses = [
    "cheddar",
    "provolone",
    "colby jack",
    "gorgonzola",
    "brief",
    "pepper jack"
]

This is the preferred way to format a list that spans multiple lines as defined by the PEP8 coding standard. PEP8 is a document available on the Web that tells Python programmers how best to format their code so that any programmer can more easily read and modify code written by others. The PEP8 document tells us this is one of the two ways that are best for defining multi-line lists. This particular way is the one we will use through the remainder of this book.

Note that we are still using commas to separate the items in the list. If we wanted to add another cheese to the end of this list, we would need to add a comma after "pepper jack" and then add the last cheese, like this:

cheeses = [
    "cheddar",
    "provolone",
    "colby jack",
    "gorgonzola",
    "brief",
    "pepper jack",
    "mozzarella"
]

This is cumbersome, so the people who invented Python decided we should be able to leave a trailing comma at the end of any list (either single line or multiple line) in case we want to add more values. This allows us to change the look of our definition to Listing 5.20 (note line 7).

Listing 5.20 List definition spanning multiple lines

cheeses = [
    "cheddar",
    "provolone",
    "colby jack",
    "gorgonzola",
    "brief",
    "pepper jack",
]

Now if we want to add "mozzarella", we can just hit the Enter or Return key and start typing. This is handy if we want to copy and paste a bunch of lines.

Listing 5.21 List definition spanning multiple lines

cheeses = [
    "cheddar",
    "provolone",
    "colby jack",
    "gorgonzola",
    "brief",
    "pepper jack",
    "mozzarella",
]

5.7. Lists of Lists

We’ve been using lists to store a series of items in a row. Each of these items can have any type: string, integer, float, … or even another list! This might sound kind of weird and scary at first, but you may be surprised to know that a list containing lists is nothing more than a matrix, a grid, a table, a spreadsheet, or whatever other term you might use to describe rows and columns of data.

Watch this:

votes = [
    [25, 18,  2],
    [19, 17,  1],
    [25,  4,  5],
    [ 5, 27, 20],
    [40, 30, 29],
]

Hey, it’s a grid! Let’s try to type some expressions using votes to see what we can do with it.

print(votes[0])      # prints [25, 18, 2]
print(votes[-1])     # prints [40, 30, 29]
print(votes[0][1])   # prints 18
print(votes[1][0])   # prints 19
print(votes[2][2])   # prints 5
print(votes[20][20]) # Kablooey!  IndexError!  The max index of votes is 4.

How does an expression like votes[0][1] work? Well, the first part of the expression votes[0] gives us the list [25, 18, 2]. Essentially, votes[0][1] becomes [25, 18, 2][1]. Then, the [1] gives us the value of the list at index 1, so [25, 18, 2][1] becomes 18.

When we use two sets of square brackets, the first square bracketed value selects the row number and the second bracketed value selects the column, as in votes[row][column].

Now, let’s see a practical example. I’ve named this list of lists votes for a reason. Suppose we have an election and we want to keep track of the votes for each candidate. Suppose we also want to be more detailed in tracking votes, so we want not just total votes but votes by county in a particular state. Let’s let the columns represent the candidates. Since we have three columns, that must mean we have three candidates! Then, let’s let the rows represent the counties. We have five rows, so we should assume we have five counties we are tracking.

So, let’s see who won the election. No Electoral College here folks; we’ll count raw votes. Let’s total them up. Only, let’s do it like real programmers. We could write total0 = votes[0][0] + votes[1][0] + votes[2][0] + votes[3][0] + votes[4][0], but that’s really lame and we’d have to change our totaling code if we ever add more counties. So, let’s do this instead (Listing 5.22).

Listing 5.22 Total votes for one candidate

total = 0
for countyindex in range(0, len(votes)):
    total = total + votes[countyindex][0]

print("Total votes for candidate 0: %d" % total)

Then, we could copy and paste this code for candidates 1 and 2, or we could put all of this code in another loop and “loop through” the candidates (Listing 5.23).

Listing 5.23 Total votes for all candidates

for candindex in range(0, len(votes[0])):
    total = 0
    for countyindex in range(0, len(votes)):
        total = total + votes[countyindex][candindex]

    print("Total votes for candidate %d: %d" % (candindex, total))

Let’s stop referring to the candidates as “Candidate 0”, “Candidate 1”, etc. Let’s give them actual names and store them in code somewhere. How about a using a list?

Listing 5.24 A list for candidates

candidates = ["Ronald Rump", "Billary Blimpton", "A Giant Meteor"]

Similarities of these names to candidates in recent U.S. presidential elections is purely coincidental… or not.

Now, check this out. See how we can use a loop with this new candidates list to label the columns of our votes grid when totaling up the results (see Listing 5.25).

Listing 5.25 Total votes for all candidates, with names

votes = [
    [25, 18,  2],
    [19, 17,  1],
    [25,  4,  5],
    [ 5, 27, 20],
    [40, 30, 29],
]
candidates = ["Ronald Rump", "Billary Blimpton", "A Giant Meteor"]
for candindex in range(0, len(votes[0])):
    total = 0
    for countyindex in range(0, len(votes)):
        total = total + votes[countyindex][candindex]

    print("Total votes for %s: %d" % (candidates[candindex], total))

The output of Listing 5.25 is:

Total votes for Ronald Rump: 114
Total votes for Billary Blimpton: 96
Total votes for A Giant Meteor: 57

This code is pretty slick. This code is also a good example of where we should be heading as programmers. We should be getting pretty comfortable with iterating through a list using a loop.

What makes this code slick? Well, if we change the structure of the votes grid, the code still works perfectly. In other words, we could add or subtract candidates, or we could add or subtract counties, and the code still works because we have not hard-coded the number of candidates or counties.

To verify this, let’s redefine votes (and candidates, so that its length matches the number of columns in votes) and then try to run our code again. A new, full listing can be found in Listing 5.26.

Listing 5.26 Total votes for all candidates, again

votes = [
    [25, 18,  4,  2],
    [19, 17,  8,  1],
    [25,  4,  1,  5],
    [ 5, 27, 21, 20],
    [40, 30,  5, 29],
    [10, 12,  1,  1],
]
candidates = ["Ronald Rump", "Billary Blimpton",
              "Johnny Third-Party", "A Giant Meteor"]
for candindex in range(0, len(votes[0])):
    total = 0
    for countyindex in range(0, len(votes)):
        total = total + votes[countyindex][candindex]

    print("Total votes for %s: %d" % (candidates[candindex], total))

Because we have not hard-coded the lengths of the lists, and because the number of votes columns matches the length of candidates, the code works as shown below.

Total votes for Ronald Rump: 124
Total votes for Billary Blimpton: 108
Total votes for Johnny Third-Party: 40
Total votes for A Giant Meteor: 58

Poor Johnny Third-Party – the Giant Meteor got more votes than he did. Maybe Johnny should re-think his political career aspirations if he can’t manage to beat an eschatological, extra-terrestrial projectile of doom!

Spend a little time thinking about how you might write code to do different things with votes and candidates. How many different ways can we slice-and-dice this data? In Section 5.10 (the Chapter 5 Exercises), you’ll be asked to report the winner of each county, and you’ll need to give each county a name. Be thinking about how you might accomplish that.

5.8. (Optional) Functional Programming with Lists

It’s not uncommon to have a list that contains items that we wish to modify. Or, we may have a list, and we wish to create a new list based on the original list. You may recall an exercise in a previous chapter where we were asked to create a program that translated English into Pig Latin. If you do not recall this exercise, it is sufficient to understand that an English word can be translated into the fictional “Pig Latin” language by taking the first consonant in the word, moving it to the end of the word, and then adding “ay” to the end. Thus, “cat” becomes “at-cay.” There are other pertinent rules for forming Pig Latin words, but for the example that follows, this understanding is sufficient.

If we take a string containing an English sentence and we transform it into a list of words, creating a program that translates English to Pig Latin becomes as simple as creating a new list from our original list where each word has been translated into its Pig Latin equivalent. Written another way, suppose we have a list like this:

words = ["jim", "likes", "radishes"]

And we wish to make a new list that looks like this:

pig_words = ["im-jay", "ikes-lay", "adishes-ray"]

We could easily write a function to translate a single word at a time. Consider the following simple function.

def piglatin(english):
    return english[1:] + "-" + english[0] + "ay"

Then, we could construct a new list by using this piglatin function on each item in the original list. Observe:

sentence = input("Enter a sentence: ")
# sentence is now something like "jim likes radishes"

words = sentence.split()
# words is now something like ["jim", "likes", "radishes"]

pig_words = []
for word in words:
    pig_word = piglatin(word)
    pig_words.append(pig_word)

There is a far more concise way to do this in Python using something called functional programming. Observe that all we wish to do is make a new list from an original list by applying a function to each item in the list. The original list is words. The new list is pig_words. The function is named piglatin. We can compress the above code into the following code.

sentence = input("Enter a sentence: ")
# sentence is now something like "jim likes radishes"

words = sentence.split()
# words is now something like ["jim", "likes", "radishes"]

pig_words = list(map(piglatin, words))

Look at the last line of the above code. This statement tells Python to “map” the function piglatin onto all of the items in words. That is, it tells Python to pass each of the items in words to piglatin, and then take all the return values and make a new list out of them.

The expression map(piglatin, words) creates something that is like a list. We then must convert its return value to a list. Notice that map takes two arguments. The second is a list, but the first is actually a function. We can pass function as parameters to other functions. Python allows us to do this because we can store a reference to a function in any variable, including parameter variables.

To understand how to pass a function to another function, consider the following “toy” example.

def call_function(func, val):
    return func(val)

call_function(print, "Hi there")
# prints "Hi there"

def square(x):
    return x * x

y = call_function(square, 3)
print(y)
# prints 9

call_function takes the first parameter func and calls it. It uses val as the argument to func.

Consider (roughly) how map works.

def map(func, inlist):
    outlist = []
    for item in inlist:
        outlist.append(func(item))
    return outlist

We say this is how map works “roughly” because map does not actually return a list; it returns something like a list that we can convert to a list. The reason for this is beyond the scope of this book.

The map function is pretty slick! Consider the following examples.

xs = ["1", "2", "3"]
ys = list(map(int, xs))
# ys is now [1, 2, 3]

strings = ["cheese", "ate", "sand"]
lengths = list(map(len, strings))
# lengths is now [6, 3, 4]

This is really the tip of the iceberg when it comes to functional programming! This is just a taste, and most other programming languages support some form of functional programming. There are a lot more things you can do with functional programming that are super powerful and really concise in terms of coding. If you take future computer science classes and read more books, it is likely you’ll encounter functional programming again. Functional programming is used frequently in “real world” code. In fact, Google’s data processing pipeline is built around a functional programming paradigm known as “Map-Reduce.” Google it!

5.9. (Optional) List Comprehensions

Based on what we know so far, we can construct lists in two ways. If we know the items we want in a list at the time we create the list, we can do so as follows.

mylist = [1, 2, 3, 4, 5]

Alternatively, we could create an empty list and then add items to it later, like this.

mylist = []
# Then, later on...
mylist.append(1)
mylist.append(2)
mylist.append(3)
mylist.append(4)
mylist.append(5)

There is an additional way to create lists that is somewhat unique to Python. This method is called a list comprehension. Consider the following code.

squares = []
for num in range(0, 10):
    squares.append(num**2)
# squares is now [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

The list comprehension-way to write this is:

squares = [num**2 for num in range(0, 10)]

A list comprehension consists of square brackets containing an expression followed by a loop that gives the expression a sequence of values. The loop can contain additional loops or even if statements. Consider this:

evens = [x for x in range(0, 16) if x % 2 == 0]
# evens is now [0, 2, 4, 6, 8, 10, 12, 14]

The value for each item in evens is x, but only if x is divisible by 2. The if expression can be used to “filter” items in the list.

List comprehensions can be handy if you have one list and you wish to make another new list based the values in the first list. For example:

sentence = "Sheamus Shaughnessy is HUNGRY."
words = [w.lower().replace(".","") for w in sentence.split()]
# words is now:
#     ['sheamus', 'shaughnessy', 'is', 'hungry']

Another example:

nonprimes = [y for x in range(2, 8) for y in range(x*2, 50, x)]
primes = [x for x in range(2, 50) if x not in nonprimes]
# primes is now:
#     [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]

Neat-o burrito!

(Mmm… burritos. Those who happen to be in Storm Lake, Iowa, may want to take a break from studying and head to La Juanitas for some exceptional, authentic Mexican food.)

5.10. Exercises

1. Suppose we define a list as follows:

   mylist = [1, 3, 5, 7, 9, 11]
   

   What is the type and value of each of the following expressions?

   mylist[1]
   mylist[0]
   mylist[-1]
   mylist[len(mylist)-1]
   mylist[1:3]
   mylist[3:]
   mylist[:3]
   7 in mylist
   8 in mylist
   len(mylist)
   sum(mylist)
   min(mylist)
   max(mylist)
   mylist[mylist[1]]
   str(mylist[2])
   ",".join(["cat", "dog"])
   

2. What is the output of the following code?

   xs = [1, 3, 5]
   ys = xs
   xs.append(7)
   ys.append(9)
   print(xs)
   print(ys)
   ys = xs[:]
   ys.remove(9)
   ys.pop(0)
   print(xs)
   print(ys)
   

3. Define a function named biggest that takes a list of numbers as a parameter and returns the biggest number in the list.

4. Define a function named average that takes a list of numbers as a parameter and returns the mean/average of the numbers as a float.

5. Define a function named contains_chuck that takes a list of names and returns True/False whether "Chuck Norris" or "Carlos Norris" is in the list.

6. Define a function named count_chucks that takes a list of names and returns an integer representing the number of names that start with "Chuck" in the list.

7. Define a function named cull_cullens that takes a list of names and returns a new list based on the original list, only in the new list any name ending in "Cullen" has been removed. For example:

   in = ["Sarah James", "Edward Cullen", "Mary Smith",
         "Bella Cullen"]
   out = cull_cullens(in)
   # out contains only ["Sarah James", "Mary Smith"]
   

8. Define a function named replace that takes a list of values, an “old” value, and a “new” value. The function should modify the list of values by replacing any “old” values with the “new” value. For example:

   game = ["duck", "duck", "grey duck", "duck", "grey duck"]
   replace(game, "grey duck", "goose")
   print(game)
   # This should print ["duck", "duck", "goose", "duck", "goose"]
   

9. Define a function named shuffle_list that takes a list as a parameter and returns a list of the same size only with the items in the parameter list in different positions. That is, the returned list should have the items randomly assigned to new positions; granted, it is possible that some of the items may still be in their original positions. For example:

   cards = ["4D", "AS", "3C", "JH", "5C"]
   new_cards = shuffle_list(cards)
   # new_cards will be different than cards, for example:
   #    ["JH", "3C", "4D", "5C", "AS"]
   

10. Define a function shuffle_this just like the function shuffle_list in the previous problem, only this time change the original list rather returning a new list. For example:

    cards = ["4D", "AS", "3C", "JH", "5C"]
    shuffle_this(cards)
    # cards will now contain something like:
    #    ["JH", "3C", "4D", "5C", "AS"]
    

11. Define a function named merge that takes two lists and returns a new single list that is the result of interleaving the two original lists. If one list is exhausted before the other, the remaining items are tacked on to the end of the resulting list. To perform the merge, the function should select the first item from the first list, the first item from the second list, the second item from the first list, the second item from the second list, etc. For example:

    new_list = merge([1, 3, 5, 7], [2, 4, 6])
    # new_list should be [1, 2, 3, 4, 5, 6, 7]
    

12. Suppose we have a list of lists (a “grid”) representing exam grades in a class. The rows are individual students’ scores. The columns are the exam scores for each student. Each score is based on a possible score of 100 points.

    Define a function named print_averages that takes a grades “grid” and a names list as parameters, and then it should print the exam average for each student along with the student’s name. The function does not need to return anything.

    NOTE: you cannot assume that there will only be three scores or three students. The code you write should still work correctly even if we were to add columns or rows. The code below serves only as an example.

    grades = [ [100.0, 98.0, 99.0],
               [ 68.5, 79.0, 85.5],
               [ 88.5, 99.0, 87.5] ]
    names = ["Samantha Beeson", "Reginald Ronald", "Dani Smith"]
    

13. Recall the votes grid example in the section on lists of lists (i.e., Section 5.7). Define a function named county_winners that prints the name of the candidate who wins each county. The output should display a line for each county. Each output line should be of the form "CANDIDATE has won COUNTY." where CANDIDATE is the candidate’s name and COUNTY is the name of the county. To define this function, you will need to create a list that stores the names of the counties in addition to defining the function body itself.

    An example of needed list definitions are:

    votes = [
        [25, 18,  2],
        [19, 20,  1],
        [25,  4,  5],
    ]
    candidates = ["Ronald Rump", "Billary Blimpton", "A Giant Meteor"]
    counties = ["Poweshiek", "Winneshiek", "Ironsheik"]
    

    Sample output:

    Ronald Rump has won Poweshiek county.
    Billary Blimpton has won Winneshiek county.
    Ronald Rump has won Ironsheik county.